一、Worley噪声原理

（细胞噪声）Cell Noise，常用来模拟细胞类有孔纹理，是一种基于Voronoi图的噪声生成算法，1996年，在Siggraph96上，Steven Worley发表的论文《A Cellular Texture Basis Function》提出了一种用于实现cellular texture方法，能有有限的资源时间内快速生成Cell噪声，因此Cell噪声也常被称为Worley噪声。

我们先来看看该算法基于的空间分割理论，在空间中，我们随机放置若干特征点（Feature points），对任一输入点P，计算其到所有特征点的距离，这个距离值的最小值就是最后的噪声值。如在上图中，蓝色点Ａ为输入点，其他所有红色点为特征点，通过计算，特征点D距离Ａ最近，所以最后的返回值为Ａ到Ｄ的距离值（0.49）。根据上面的理论，理解上非常容易，我们也可以很快的想到实现的步骤和方法如下：

１、在空间中随机产生若干特征点

２、根据输入点位置遍历所有特征点，找到输入点到所有特征点的最小距离值返回

这个算法是完全根据空间分割理论来实现的，因此逻辑上没有问题，但在真正实现时有遇到很多现实问题，一是所有空间存储特征点需要消耗巨大的存储空间，二是计算输入点到所有点的距离最小值会消耗巨大的时间，因此，上面的算法虽然逻辑可行，但实际操作不可行。

二、Worley噪声算法

因此，Steven Worley在他的论文《A Cellular Texture Basis Function》中提出了一种优化算法，这种算法同时规避了上面说的两个弊端，不需要存储特征点，只计算输入点到若干相关特征点的距离值，真正将算法实用化。

Worley算法分六步：

１、确定输入点所在的晶胞

２、对该晶胞产生可重复的随机数生成器

３、确定在该晶胞内生成特征点的数量

４、随机的将３所生成的特征点放置到晶胞中

５、计算输入点到该晶胞内所有特征点的距离最小值

６、查找并计算输入点到所在晶胞直接相邻晶胞内特征点的距离最小值，并与５中生成的最小值比较，返回最小值

三、Worley噪声算法解释

我们算法也根据Worley的方法分成六步，下面我将一一讲解

１、确实输入点所在的晶胞

这步与在Perlin噪声和Simplex噪声中一样，只需要对输入坐标进行GetFoor就可以得到左下角晶格点坐标值，也即是确定了输入点所在的晶胞

２、对该晶胞产生可重复的随机数生成器

为什么要生成可重复的随机数生成器，Worley算法基于沃罗诺伊图（Voronoi Diagram），或者说沃罗诺伊空间分割理论，按照沃罗诺伊的理论，空间中随机分布若干特征点，对Worley噪声算法来说，这些特征点是已经存在的，即需要保证在某个晶胞内的特征点分布是固定的，不能这次计算这个晶胞内三个特征点，下次计算是四个，所以在算法中我们需要一个能重复生成特征点的随机数发生器，换句话说就是不管什么时候计算，在特定晶胞内的特征点分布都是一样的，这对Worley噪声算法很重要。在我们的算法中我们使用晶胞左下角的顶点坐标值为种子生成随机数，这Hash函数就可以做到，在我们的算法里，我们使用了FNV Hash算法，这样可以保证种子的唯一性，然后我们使用之前学习的线性同余算法（LCG random number generator）作为我们随机数生成器。

３、确定在该晶胞内生成特征点的数量

理论上来讲，分布在晶胞内的特征点是由特征点在整个空间中的分布决定的。最简单的生成特征点的方法就是泊松分布（Poisson distribution），它指定空间中点的平均密度。每个点的位置独立于其他点，每个区域的点的任何数目的确切概率可用离散泊松分布函数来计算，即这些特征点随机分布在空间中且彼此之间相互独立，我们想要点的同向性分布，以避免明显的格子状的形式。出于性能的考虑，晶胞内的特征点不宜太多，我们取[1,9]，最小值取１是为了防止下步计算出问题，原理下节说明。

４、随机的将３所生成的特征点放置到晶胞中

根据泊松分布理论，我们随机的将特征点放入到晶胞中去，实现操作中，我们并不存储特征点的坐标值，因为我们只需要输入点到特征点的距离值，在取到值后没必要保留特征点坐标。

５、计算输入点到该晶胞内所有特征点的距离最小值

在步骤４中，我们在放置特征点时就一并计算了距离值，放置完所有特征点也就可以得到输入点到该晶胞内所有特征点距离的最小值。

６、查找并计算输入点到所在晶胞直接相邻晶胞内特征点的距离最小值，并与５中生成的最小值比较，返回最小值

在５中，我们计算了输入点到其所在晶胞内的所有特征点的距离最小值，但有时，输入点到空间中所有特征点的距离最小值不一定就在该晶胞内，而可能在其相邻晶胞内，如下图所示。

在上图中，输入点Ａ到所有特征点的最小距离值是Ａ与Ｂ的距离，显然此时Ａ与Ｂ不在同一个晶胞内，所以我们还必须检查输入点到所有与其邻近晶胞内特征点的距离，这就需要对其相邻晶胞也进行迭代。

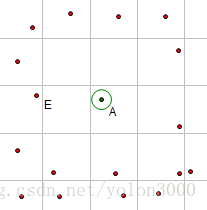
现在我们来看看在步骤３中，我们为什么将特征点数量的下限设为１，因为下限设为１才能保证输入点到所有特征点的距离最小值的那个特征点要么处于与输入点相同的晶胞内要么处于与其直接相邻的晶胞内，如果下限不为１的话将出现与输入点距离最小值的那个特征点出现在别的地方，而且没法预估其出现的晶胞，这样会导致计算无法继续，如下图所示，与输入点Ａ距离最小值的特征点为Ｅ，而Ｅ既不在与Ａ相同的晶胞内，也不在与Ａ直接相邻的晶胞内。

四、小结

在前面的学习中，我们学习过几种常见的距离算法类型，如欧几里得距离（euclidean Distance），曼哈顿距离（Manhattan Distance），切比雪夫距离（Chebyshev Distance）等等，不同的距离算法最后生成的噪声会有明显的不同。同时，我们不仅可以得到输入点到特征点的最小值，也可以得到输入点到特征点的第二小值、第三小值等，利用这些值，可以实现很多不同的噪声效果。

对任一位置x，定义F1(x)为x到其最近特征点的距离。当x变化时，F1平滑变化（因为x是平滑变化的）。但在特定端点，x可能会与2个特征点的距离相等。但这是没关系的。x连续变化时，F1值仍然连续，尽管F1的导数在计算距离从一特征点转到相邻特征点时会变化不连续。F2(x)表示x与第2近的特征点的距离。同样，可定义Fn(x)为x到第n近的特征点的距离。F函数有如下有趣的特征：

1. Fn总是连续的；

2. Fn是非减函数：0<=F1(x)<=F2(x)<=F3(x)…，通常Fn(x)<=Fn+1(x);

3. Fn的梯度为从第n最近特征点到x的单位方向向量。

参考文献

１、A Cellular Texture Basis Function，Steven Worley，Siggraph96

２、

你可能感兴趣的文章